卷积神经网络
一、卷积神经网络（CNN）
1.1 为什么用到卷积
我们刚刚讲了这个简单的神经网络，我们输入的特征值是
points = np.array( [
# [输入值, 标签值]
[0.8, 0], # 不健康（值太低）
[1.1, 0], # 不健康（值太低）
[1.7, 0], # 不健康（值太低）
[1.9, 0], # 不健康（值太低）
[2.7, 1], # 健康
[3.2, 1], # 健康
[3.7, 1], # 健康
[4.0, 1], # 健康
[5.0, 0], # 不健康（值太高）
[5.5, 0], # 不健康（值太高）
[6.0, 0], # 不健康（值太高）
[6.3, 0], # 不健康（值太高）
] )
但是由于我们之前讲计算机存储的图像的时候，图像的特征值有特别多，这里单一特征点 是一个输入，但是对于图片来说比如说32X32像素的彩色图像，每个像素点包含RGB三个通道数据，因此一张图像有32X32X3个数值（字节），如果是全连接，输入节点就需要3072个节点，假设第一层全连接层有1000个节点，那么就需要3071X1000 = 3072000 个参数，那么就需要更多的存储和计算资源，如果图片更大，那么参数量呈指数增长，这不是我们希望看到的。
比如说对于这张图片：
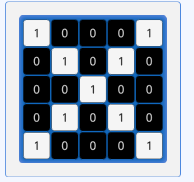这是一个经过了二值化或者灰度化的5x5的像素点图片，我们可以比较容易的看出来这一个X，同理参考下图
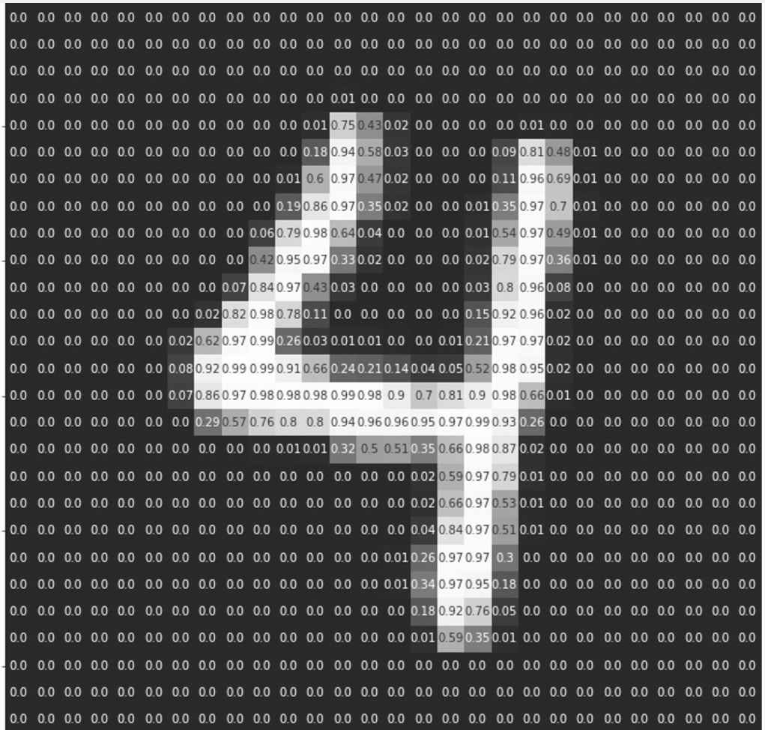计算机中存储的数字4，作为人来说，也可以很好的观察出来这是数字4。
可以说全连接除了参数太多的问题之外，对于我们还可以根据图片的三维特征来判断图片，而对于单纯的全连接网络来说，它的输入都是一维的。一个3维的图像的形状，应该含有重要的空间信息。比如空间上邻近的像素为相似的值、BGR的各个通道之间分别有密切的关联性、相距较远的像素之间没有什么关联等，3维形状中可能隐藏有值得提取的本质模式。
因为全连接层会忽视形状，将全部的输入数据作为相同的神经元
（同一维度的神经元）处理，所以无法利用与形状相关的信息。
卷积层可以保持形状不变。当输入数据是图像时，卷积层会以 3 维
数据的形式接收输入数据，并同样以3 维数据的形式输出至下一层。