一、人工智能简介

1.1 人工智能发展历史

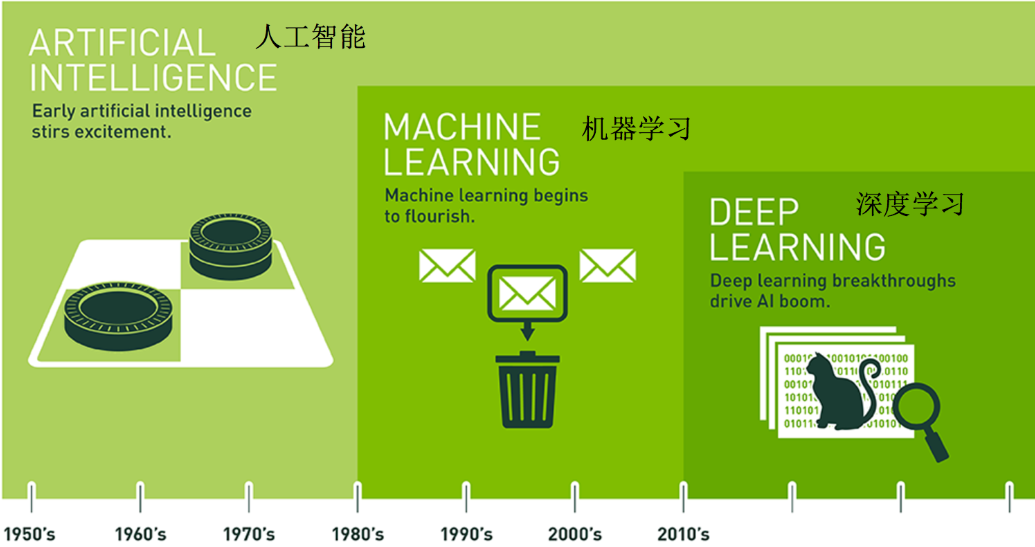
1.1.1 早期的人工智能

早期的人工智能：在这个阶段，人工智能主要关注逻辑和规则基础的系统，这些系统能够执行一些基础的推理和问题解决任务。这个时期的AI系统通常被称为“专家系统”，它们可以处理分类问题，但它们的应用范围相对有限。

[!NOTE] 智能对话助手： ”我发烧了“ --- ”你可能需要看医生“ “我饿了，而且喜欢甜食” --- “你可能会喜欢巧克力。” “饿了”对应“吃东西”，“冷了”对应“穿衣服” 基于固定的规则来给出答案，不能处理复杂的问题，比如我肚子疼，但是不想吃药，怎么办？

1.1.2 机器学习

机器学习：机器学习的发展使得AI系统能够从数据中学习并做出预测或决策，而不仅仅是依赖于硬编码的规则。机器学习算法可以处理包括分类在内的各种任务，如回归、聚类、强化学习等。在这个阶段，算法开始能够根据给定的特征自动发现模式并进行分类。

[!NOTE] 智能对话助手： 可以通过不同的特征，进而解决复杂的问题，比如我肚子疼，但是不想吃药，怎么办？

下面我们来简单了解常常会听到几个机器学习算法。

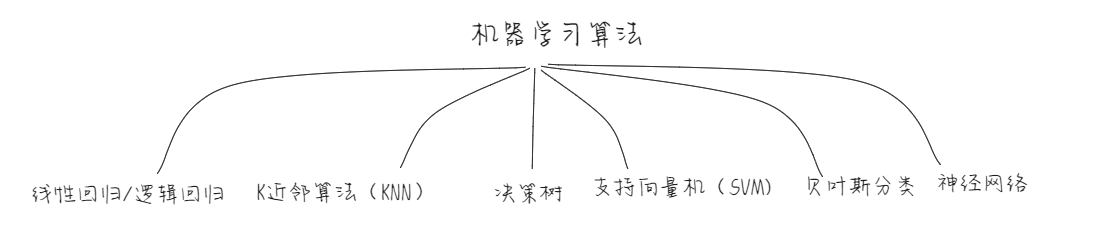
1.1.2.1 线性回归/逻辑回归

AI的智能主要就是做两件事情：回归和分类 回归：预测一个具体的值，比如预测你的身高185CM、体重75KG、毕业后收入100万 分类：判断你是男女、胖瘦、学生还是老师

线性回归：找到一条线，来预测一个具体的值。 假设我们想要根据房屋的面积来预测房屋的价格。我们收集了一组房屋的数据，包括房屋面积和对应的销售价格。

房屋面积（平方米）	房屋价格（万元）
80	120
100	150
120	180
140	210
160	240
通过线性回归分析，我们试图找到一条直线方程来表示房屋面积和价格之间的关系。假设这个方程为 y = ax + b，其中 y 表示房屋价格，x 表示房屋面积，a 和 b 是待确定的参数。
利用线性回归算法，可以计算出最适合这些数据的 a 和 b 的值。比如经过计算可能得到 a = 1.5，b = -10，那么线性回归方程就是 y = 1.5x - 10。
现在如果有一套新的房屋，面积是 110 平方米，我们就可以利用这个线性回归方程来预测它的价格。将 x = 110 代入方程，得到 y = 1.5×110 - 10 = 155（万元）。
所以，通过线性回归，我们找到了一条线（方程）来预测房屋的具体价格。

如果我们把预测出来的房屋的具体价格进行划分，比如200万的以上的房子叫做豪宅、200万以下的叫做改善型住宅。那么我们就做了一个分类，这个我们称之为逻辑回归。虽然这个被称为回归，但是解决的是分类问题。

线性回归和逻辑回归本质上就是使用损失函数（y=wx+b）找到坐标轴中的那一条线的过程。

1.1.2.2 K近邻（KNN)

K近邻一般也是用来解决分类问题，K近邻的基本思想可以概况为8个字---物以类聚，人以群分。 假设我们要根据水果的两个特征 —— 大小和颜色鲜艳程度，来判断水果是苹果还是橙子。 我们有以下已知数据：

水果	大小	颜色鲜艳程度	类别
水果 1	中等	较鲜艳	苹果
水果 2	大	鲜艳	苹果
水果 3	小	不太鲜艳	橙子
水果 4	中等	不太鲜艳	橙子
在 K 近邻算法中，“K = 3” 表示选取距离待分类样本最近的 3 个已知样本。
现在有一个新的未知水果，大小为中等，颜色鲜艳程度为较鲜艳。
我们使用 KNN 算法，假设 K = 3。首先计算新水果与已知水果的距离（可以使用欧氏距离等方法）。计算后发现距离新水果最近的三个水果为水果 1、水果 2 和水果 4。其中水果 1 和水果 2 是苹果，水果 4 是橙子。由于苹果的数量占多数，所以根据 “物以类聚，人以群分” 的思想，我们判断这个新水果是苹果。

1.1.2.3 决策树

比如用决策树来判断是否会购买某款电子产品的例子 影响因素有：产品价格、品牌知名度、产品功能丰富度。 我们先有一些已知数据：

产品价格（高 / 中 / 低）	品牌知名度（高 / 中 / 低）	产品功能丰富度（高 / 中 / 低）	是否购买
高	高	高	是
中	高	中	是
低	中	低	否
高	低	中	否
中	中	高	是
低	低	低	否
电脑首先尝试产品价格这个节点。假设分为高价格、非高价格（中低价格合并）两类，高价格组中有购买和不购买两种情况，假设购买比例为 50%；非高价格组中也有购买和不购买两种情况，假设购买比例为 33.3%。通过计算可以发现，单纯以产品价格分类的分类纯度不是很高。

接着尝试品牌知名度节点。分为高知名度、非高知名度两类，高知名度组中购买比例较高，假设为 75%；非高知名度组中购买比例较低，假设为 25%。分类纯度有所提高。

再尝试产品功能丰富度节点。分为高丰富度、非高丰富度两类，高丰富度组中购买比例较高，假设为 80%；非高丰富度组中购买比例较低，假设为 20%。分类纯度进一步提高。

电脑比较各个节点的分类纯度后，将产品功能丰富度放在较接近根节点的位置，品牌知名度次之，产品价格放在相对较靠下的位置。最终生成的决策树可能如下：

如果产品功能丰富度高，那么很可能购买；如果产品功能丰富度低，再看品牌知名度，如果品牌知名度高，有一定可能购买；如果品牌知名度低，再看产品价格，如果产品价格高，不太可能购买，如果产品价格低，也不太可能购买。

这样生成决策树后，就可以用它来预测新的数据，比如对于一个新的电子产品，根据其产品价格、品牌知名度和产品功能丰富度，利用决策树判断是否会被购买。

[!NOTE] 分类纯度简单来说，就是使用这个影响因素来分类，分类之后的每个分类的数据一致性有多高。比如如果我们使用染色体特征来分类男女，纯度是最高的，分类得到的数据中一致性是100%，也就是分类得到的男生和女生其中的数据一致性最高，但是按照其他的影响因素比如是否穿裙子来进行划分，那么男生组中可能会有15%的女生，女生组中可能有10%的男生。

1.1.2.4 支持向量机（SVM）

上个世纪末，支持向量机就是最牛的机器学习算法。支持向量机理论在1963年就被提出来了，支持向量机有着优雅的结构和算法，同时也超级难搞。

比如现在还是有苹果和橙子两个水果。

水果	大小	颜色鲜艳程度	类别
水果 1	中等	较鲜艳	苹果
水果 2	大	鲜艳	苹果
水果 3	小	不太鲜艳	橙子
水果 4	中等	不太鲜艳	橙子
支持向量机就是通过数学方法找到最宽的那一条沟，新的数据如果落在数据的一侧就是苹果，另一侧就是橙子。而这条沟被我们称为超平面。沟边缘的橙子和苹果就被叫做支持向量。
到这里为止看起来和之前的线性回归很类似，但是支持向量机有一个不同，可以解决线性不可分问题。

坐标系中的一堆数据，画一条直线下去，能分成两半，就叫做线性可分问题，如果不能分成两半，就叫做线性不可分问题。二维以上同理。

水果	大小	颜色鲜艳程度	类别
水果 1	中等	较鲜艳	苹果
水果 2	大	鲜艳	橙子
水果 3	小	不太鲜艳	橙子
水果 4	中等	不太鲜艳	苹果

支持向量机的解决方法就是升维。 引入甜度的这个影响因素：

水果	大小	颜色鲜艳程度	甜度	类别
水果 1	中等	较鲜艳	高	苹果
水果 2	大	鲜艳	低	橙子
水果 3	小	不太鲜艳	低	橙子
水果 4	中等	不太鲜艳	高	苹果

这样就可以找到一个平面将其划分开来。 一般来说，新添加的影响因素是与前面的影响因素有关系，比如z=x^2+y^2 这个可以将空间升维的函数被称之为核函数。核函数有很多种，不同的情况需要使用不同的核函数。但是他的作用就是使得数据升维，实现线性可分。

1.1.2.5 朴素贝叶斯

朴素贝叶斯常常用来做分类，比如在已知的某些症状的前提下，判断是否得了某种疾病。”浑身发热，还有咳嗽，是不是得了新冠“。 或者已知关键词的情况下，判断某篇文件的分类或者某封邮件是不是垃圾邮件。 ”量子计算“ ”人工智能“ ”DNA“ --- 科技类 ”紫薇等一下“ ”大碗牢饭“ --- 搞笑类 ”我爱你“ ”浪漫主义“ ”莎士比亚“ --- 文学类

”脑袋大，脖子粗，不是大款就是伙夫“ ---- 赵本山 这是典型的朴素贝叶斯分类法

排除先验概率—后验概率 — 公式这种复杂的解释： 假设长的帅的人，有98%的概率有女朋友，90%的概率会来上课，80%的概率会编程。那么一个人既有女朋友，又来上课，同时也会编程，那么他大概率长的帅。这就是朴素贝叶斯。 根据某一些事件的概率，来反推当这些事件发生的时候，他是某一类事物。

1.1.3 神经网络

1957年弗兰克 罗森布拉特提出感知机的概念。但现在我们往往称它为深度学习。

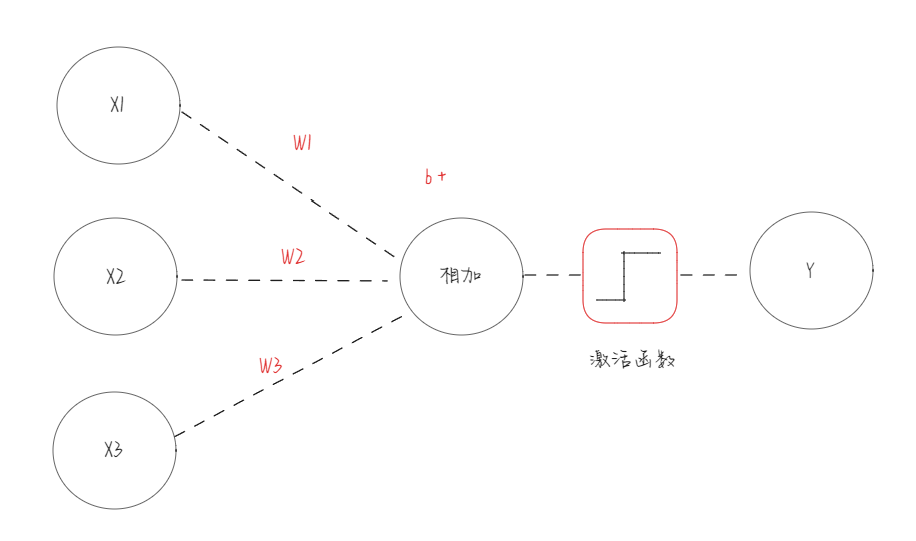
基本思想是模拟大脑的神经元的工作方式，来构造预测函数和损失函数。 单个感知机的算法机制其实就是在模拟大脑神经元的运行机制。 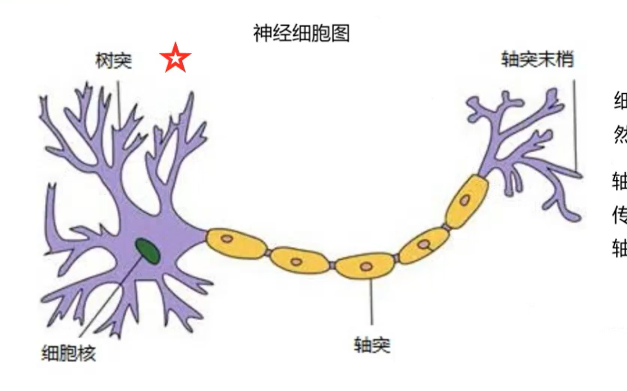把上面这张图抽象成下面的样子：

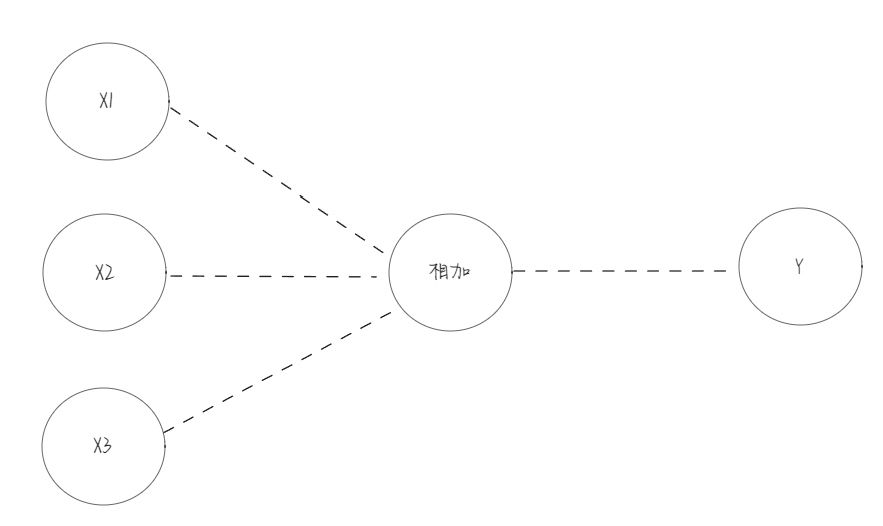
如果转换成数学公式：X1+X2+X3 = Y 就是这样的公式导致了人机大战（围棋对弈）、引发AI替代人类的思考。

我们需要理解如何基于这个公式来构建整个神经网络，也就是如何利用最简单的公式来构建复杂的系统。

神经元的每一个树突不断的接受输入信号，但不是每一个输入信号都能让轴突输出信号的，每一个树突在输入的时候占有的权重也是不同的。 上面的公式做一下优化： Y = W1*X1+W2*X2+W3*X3 + b

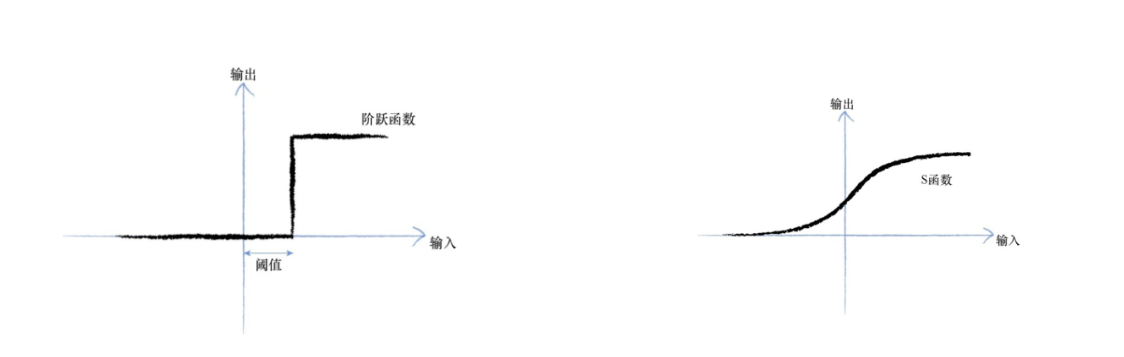
观察表明：神经元不会立即做出反应，而是会抑制输出，直到输入增强，强大到可以触发输出。

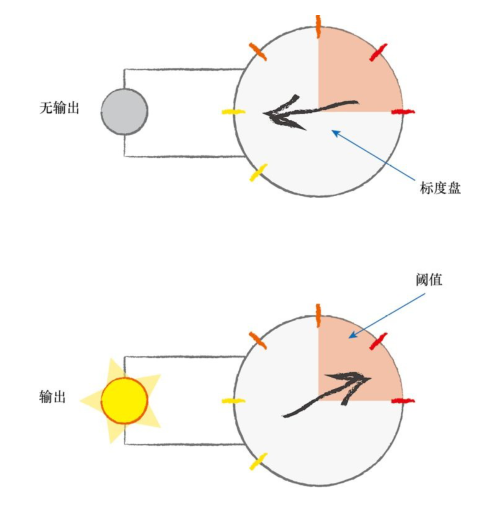
考虑到这个阈值的特性，我们引入激活函数的概念。

上述的激活函数有很多样子，后面这个S型的函数，一般称为S函数（sigmoid函数）

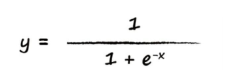
二、神经网络详解

2.1 单个感知机的问题

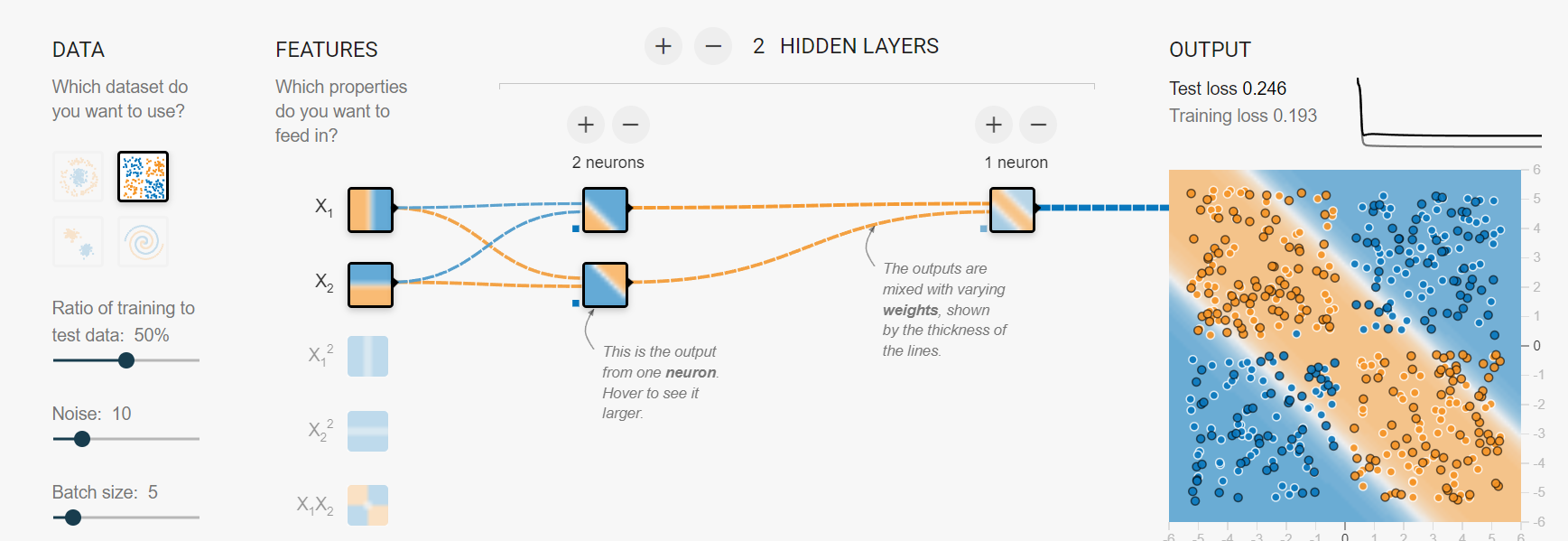
https://playground.tensorflow.org/ 通过刚刚讲解的神经网络的发展，对于单个感知机本质就是画了一条线，把两种不同的东西分开。 比如说我们有一个数据集

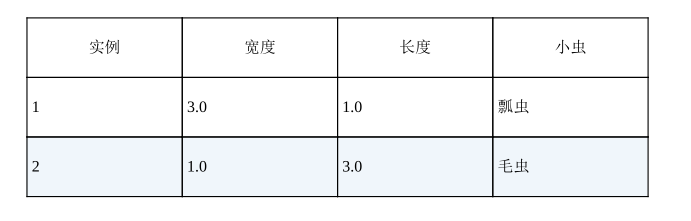
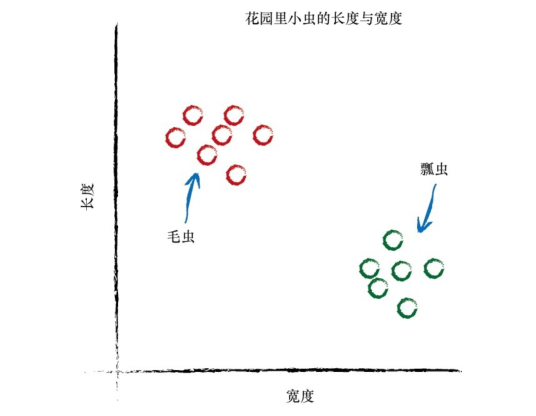
单个感知机可以解决线性可分问题，但是对于线性不可分问题就无能为力了。

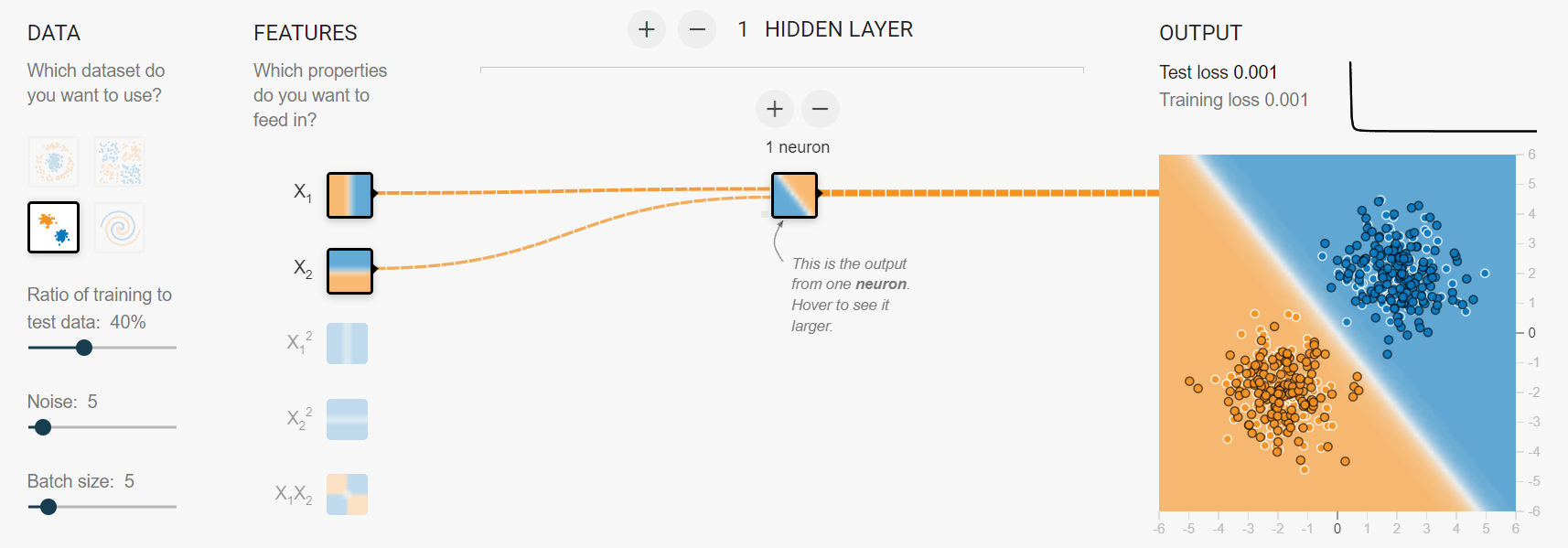
而对于线性不可分问题，在计算机中有一个基本的运算：异或；

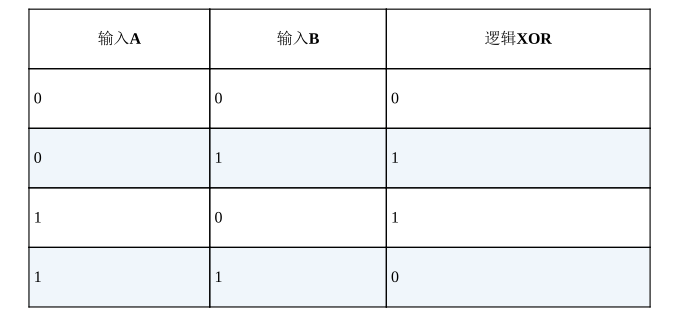
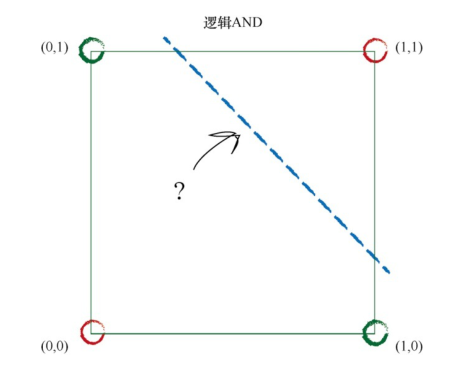单个感知机异或问题都无法解决，就会导致它的实用性大大降低。

解决这个问题，有同学会说，参考支持向量机（SVM）直接升维，但是支持向量机刚刚起步，所以也还没有大放异彩。

但是感知机走出了另一条路：加层；

对于异或运算，这种复杂运算可以拆分成较为简单的运算：

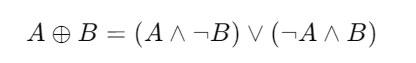
A 异或 B = (A取反 与 B) 或 （A 与 B取反）

这样就解决了异或问题，同时也解决了线性不可分问题。同时对于复杂性的问题，这个方式都可以做解决，从此就开启了神经网络的发展。

2.2 神经网络如何工作

2.2.1 数据集

使用最简单的神经网络来举一个例子：

我们首先来观察一下数据集：

points = np.array( [ # [输入值, 标签值] 
			[0.8, 0], # 不健康（值太低） 
			[1.1, 0], # 不健康（值太低） 
			[1.7, 0], # 不健康（值太低） 
			[1.9, 0], # 不健康（值太低） 
			[2.7, 1], # 健康 
			[3.2, 1], # 健康 
			[3.7, 1], # 健康 
			[4.0, 1], # 健康 
			[5.0, 0], # 不健康（值太高） 
			[5.5, 0], # 不健康（值太高） 
			[6.0, 0], # 不健康（值太高） 
			[6.3, 0], # 不健康（值太高） 
] )

我们想实现 给这个神经网络一个值，它给我返回一个是否健康的值，可以看出来靠近0代表不健康，靠近1代表健康。

2.2.2 权重

权重刚开始可以给一个任意的值，因为后面会不断更新它的值。

# 参数初始化
w11_1 = 0.1
b1_1 = 0.6
w12_1 = 0.9
b2_1 = 0
w11_2 = -1.5
w21_2 = 0.1
b1_2 = 0.9

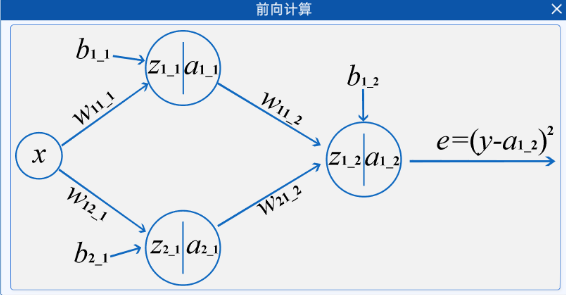
2.2.3 计算过程

接下来我们就可以开始计算了：

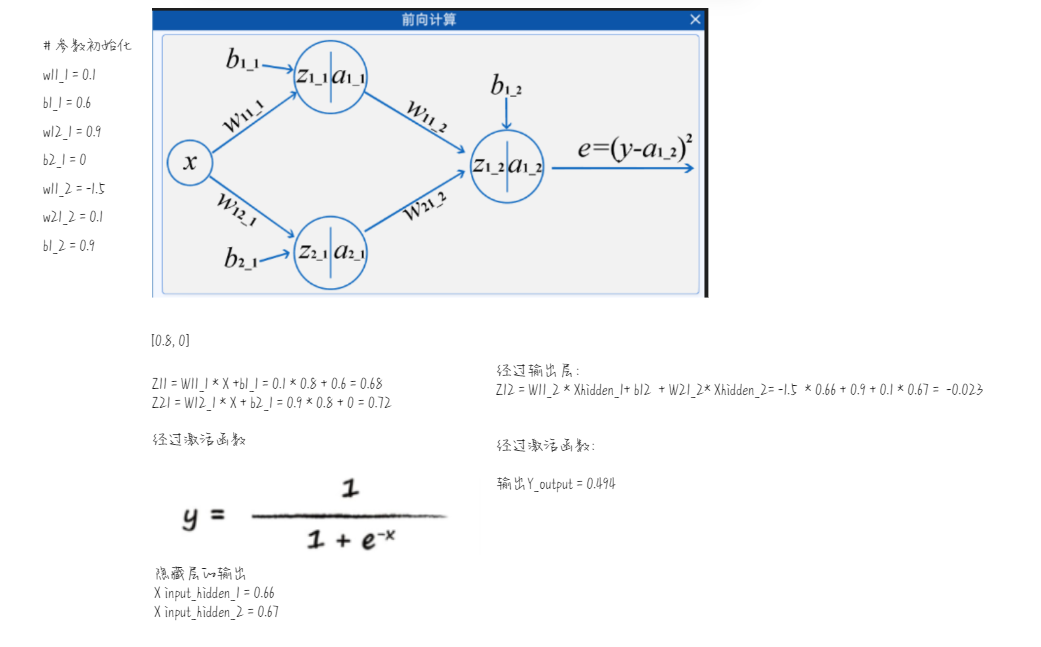
计算出来的结果和实际的值有差距，接下来我们就可以使用这个误差来更新权重。

2.2.4 利用误差更新权重

如何利用误差来更新权重，首先我们一个简单的例子：

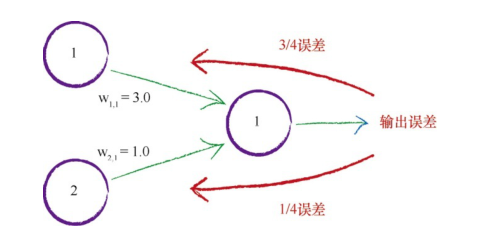
利用权重，将误差从输出向后传播到网络中，我们称这个方法为反向传播。

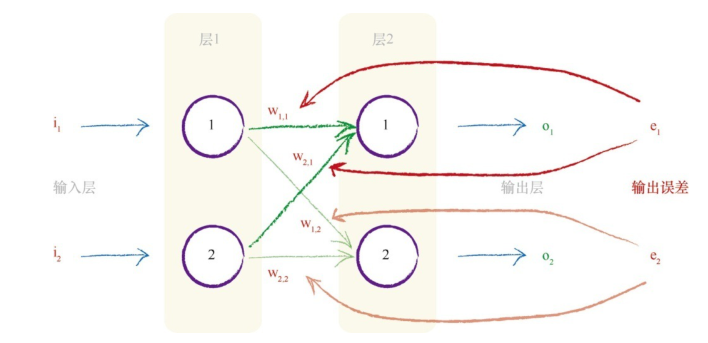
现在我们已经知道如何分配得到的误差了，但是还有两个问题：

1. 对于更远端的权重如何更新？
2. 如何利用得到的误差更新权重，加？减？还是其他的复杂运算

对于更远端的的权重如何更新？

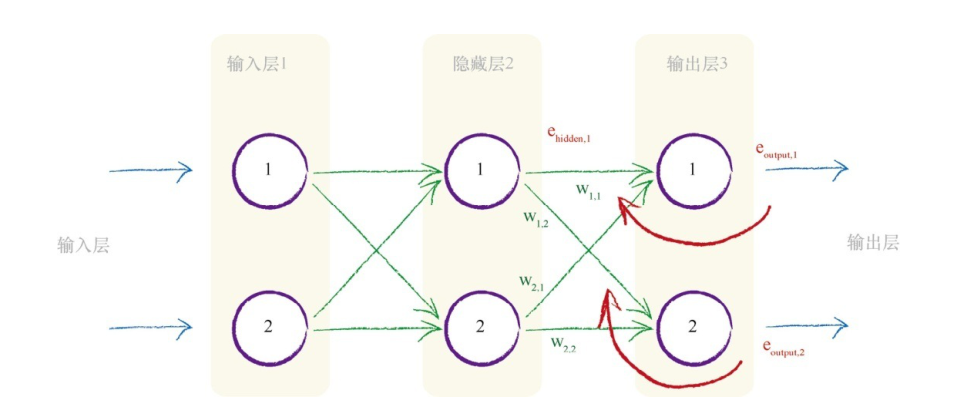
这样就得到了隐藏层第一个节点的”误差“，这个”误差“不是一个真实的定义，因为对于隐藏层来说，输出的数据其实没有什么误差的概念。利用这个误差就可以继续向前推导了。

如何利用得到的误差更新权重，加？减？还是其他的复杂运算

我们不能利用简单的代数运算来更新权重，因为我们不确定如何调整输入层和隐藏层的权重，进而使得输出层的节点的输出增加0.5或者减少0.5。 那么如何来更新呢？ 首先第一件事情：悲观主义。 训练数据不足、训练数据可能有错误、神经网络有缺陷、没有足够的层或者节点不能对问题进行建模等等，这些都会导致很难找到最好的组合。

接下来，我们来更新权重： 首先第一步选择误差函数（损失函数），我们的目的是调整权重让误差最小，很容易就能想到这其实是利用函数求最小值的一个过程。

网络输出	目标输出	误差 (目标值 - 实际值)	误差(|目标值 - 实际值|)	误差 (目标值 - 实际值)²
0.4	0.5	0.1	0.1	0.01
0.8	0.7	-0.1	0.1	0.01
1.0	1.0	0	0	0
求和		0	0.2	0.02
最容易想到的就是第一种公式 e = 目标值 - 实际值。但是它会出现经过几次求和之后，误差为0 的情况。
第二种公式，由于斜率在最小值附近不是连续的，这使得梯度下降方法无法很好地发挥作用，由于这个误差函数，我们会在V形山谷附近来回跳动。
第三种被称为均方误差（MSE），这是常见的损失函数，参考下图

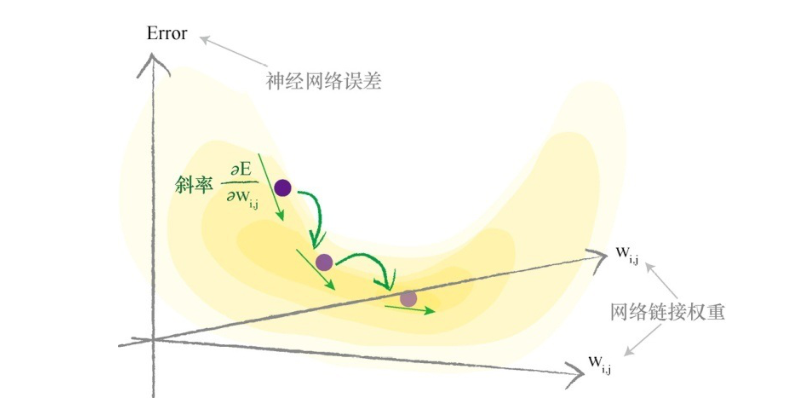
接下来就变得简单起来了，就是根据方程对权重求偏导，找到最小的误差。 这里利用链式求导法则开始求导

接下来依次对权重求导：

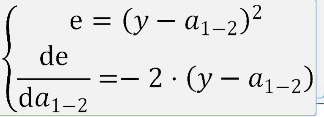
下面出现了sigmoid函数，得益于数学家的功劳，针对sigmoid函数的导数：

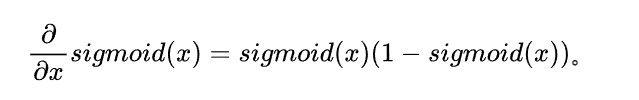
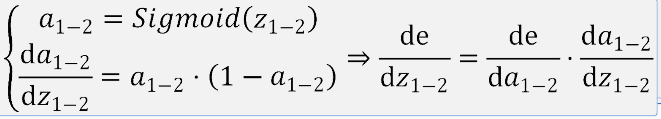
接下来就是对权重W11_2的导数 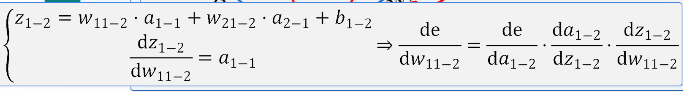汇总得到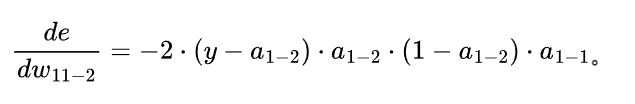： 其中a1-2 是输出层节点的输出 a1-1是上一个节点的输出

这样就计算出来了斜率，当然这个斜率我们也不会直接使用，而是利用上面的数据集，输入数据集中每一个特征值都会输出一个误差，然后都可以算出一个误差的斜率，我们把这个斜率求和最后取平均值，得到一个平均斜率，这是常见的一种归一化操作。 这样做可以避免在不同数量的样本下，梯度的大小差异过大。如果不进行归一化，当样本数量较多时，梯度可能会变得很大，导致权重更新幅度过大，可能会使训练过程不稳定；而当样本数量较少时，梯度可能会很小，导致权重更新缓慢。

然后开始计算新的权重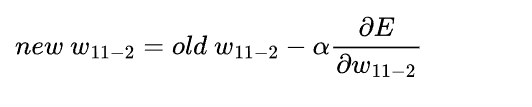： 这里也可看到，如果斜率是负的，那么就在原来的权重上增加点，如果是斜率是正的，就在原来的权重上减小点，其中α被叫做学习率，用来确保调节的强度，避免超调的。以上就更新好了一个权重，其他权重同理。

下面再看一个偏置（b常数）是如何被更新的： 前两步和上面相同，最后一步是对b1_2的偏导：

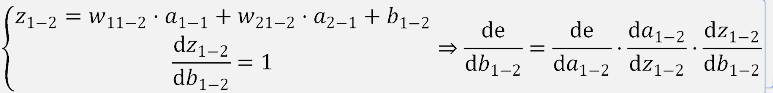
汇总得到：

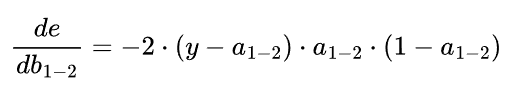
之后同理对b1-2进行更新。

经过较多次的迭代，会将模型训练完成。

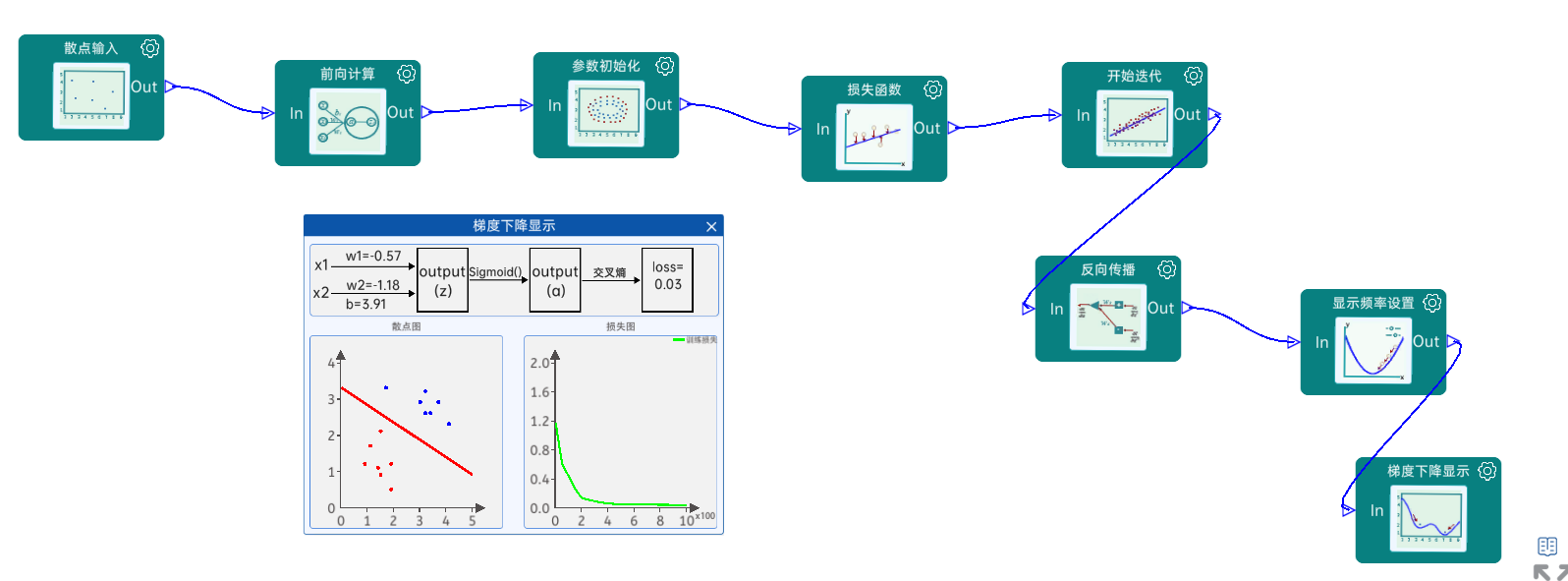
2.2.5 实验代码

# 导入相关库
import numpy as np
from IPython import display
import matplotlib.pyplot as plt

# 定义激活函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))


# 1.散点输入
points = np.array([[0.8, 0], [1.1, 0], [1.7, 0], [1.9, 0], [2.7, 1], [3.2, 1], [3.7, 1], [4.0, 1], [5.0, 0], [5.5, 0], [6.0, 0], [6.3, 0]])

# 将输入特征和标签值分开（x是输入特征，y是真实标签值）
X = points[:, 0].reshape(-1, 1)
y = points[:, 1].reshape(-1, 1)
# 计算特征值的个数，反向传播求导时用
l_x_data = X.shape[0]

# 初始化图
plt.xlabel("x axis label")
plt.ylabel("y axis label")
# 定义图像的横坐标范围
x_values = np.linspace(0, 7, 100)


# 参数初始化
w11_1 = 0.1
b1_1 = 0.6
w12_1 = 0.9
b2_1 = 0
w11_2 = -1.5
w21_2 = 0.1
b1_2 = 0.9


# 超参数初始化(学习率和迭代次数)
learning_rate = 0.5


# 损失值列表，作图时使用
loss_values = []

# 4.开始迭代
num_iterations = 5000
for n in range(1, num_iterations + 1):
    # 2.前向计算
    z1_1 = w11_1 * X + b1_1
    a1_1 = sigmoid(z1_1)
    z2_1 = w12_1 * X + b2_1
    a2_1 = sigmoid(z2_1)
    z1_2 = w11_2 * a1_1 + w21_2 * a2_1 + b1_2
    a1_2 = sigmoid(z1_2)

    # 3.损失函数(均方差损失函数)
    e = np.mean((y - a1_2) ** 2)
    # 将损失值放入损失值列表中，方便图像显示
    loss_values.append(e)

    # 5.反向传播(对所有的参数进行求导)
    deda1_2 = -2 * (y - a1_2)
    dedz1_2 = deda1_2 * a1_2 * (1 - a1_2)

    dedw11_2 = (dedz1_2 * a1_1).sum() / l_x_data
    dedw21_2 = (dedz1_2 * a2_1).sum() / l_x_data
    dedb1_2 = dedz1_2.sum() / l_x_data

    deda1_1 = dedz1_2 * w11_2
    dedz1_1 = deda1_1 * a1_1 * (1 - a1_1)
    dedw11_1 = (dedz1_1 * X).sum() / l_x_data
    dedb1_1 = dedz1_1.sum() / l_x_data

    deda2_1 = dedz1_2 * w21_2
    dedz2_1 = deda2_1 * a2_1 * (1 - a2_1)
    dedw12_1 = (dedz2_1 * X).sum() / l_x_data
    dedb2_1 = dedz2_1.sum() / l_x_data

    # 梯度下降更新参数
    w11_2 = w11_2 - learning_rate * dedw11_2
    w21_2 = w21_2 - learning_rate * dedw21_2
    b1_2 = b1_2 - learning_rate * dedb1_2

    w11_1 = w11_1 - learning_rate * dedw11_1
    b1_1 = b1_1 - learning_rate * dedb1_1
    w12_1 = w12_1 - learning_rate * dedw12_1
    b2_1 = b2_1 - learning_rate * dedb2_1

    # 6.显示频率设置
    frequency_display = 100
    if n % frequency_display == 0 or n == 1:
        # 绘制拟合曲线
        z1_1_values = w11_1 * x_values + b1_1
        a1_1_values = sigmoid(z1_1_values)
        z2_1_values = w12_1 * x_values + b2_1  # 更新 z2_1 的计算，使用 b2_1
        a2_1_values = sigmoid(z2_1_values)
        z1_2_values = w11_2 * a1_1_values + w21_2 * a2_1_values + b1_2
        y_values = sigmoid(z1_2_values)

        plt.clf()  # 清空当前子图内容
        # 绘制第一个子图，内容为散点拟合曲线图
        plt.subplot(2, 1, 1)
        # 定义标题为当前步数值
        plt.title(f'Step: {n}')
        # 绘制散点
        plt.scatter(X[:, 0], y, color='red', label='Original points')
        # 绘制曲线
        plt.plot(x_values, y_values, color='blue', label='Fitted curve')
        # 显示图像中散点和曲线对应的标签
        plt.legend()

        # 绘制第二个子图，内容为损失函数曲线图
        plt.subplot(2, 1, 2)
        # 绘制曲线
        plt.plot(range(len(loss_values)), loss_values, color='green')
        # 定义横坐标的标签
        plt.xlabel('Iteration')
        # 定义纵坐标的标签
        plt.ylabel('Loss')
        # 定义标题为损失值
        plt.title('Loss Curve')
        # 定义两个子图之间的垂直距离
        plt.subplots_adjust(hspace=0.5)
        # 显示图形
        display.display(plt.gcf())
        # 清空Jupyter输出
        display.clear_output(wait=True)

# 定义预测函数，输入新的x值，输出预测的y值
def predict(x_new):
    z1_1 = w11_1 * x_new + b1_1
    a1_1 = sigmoid(z1_1)
    z2_1 = w12_1 * x_new + b2_1
    a2_1 = sigmoid(z2_1)
    z1_2 = w11_2 * a1_1 + w21_2 * a2_1 + b1_2
    a1_2 = sigmoid(z1_2)
    return a1_2

# 测试数据
x_test = np.array([[1.5], [2.5], [3.5], [4.5], [6.5]])

# 对新数据进行预测
y_pred = predict(x_test)

# 输出预测结果
print("输入特征:", x_test.flatten())
print("模型预测:", y_pred.flatten())